常用的几种排序

Admin
算法
17 Jul, 2022

排序算法是《数据结构与算法》中最基本的算法之一。也是数据结构和算法入门必须掌握了解的知识

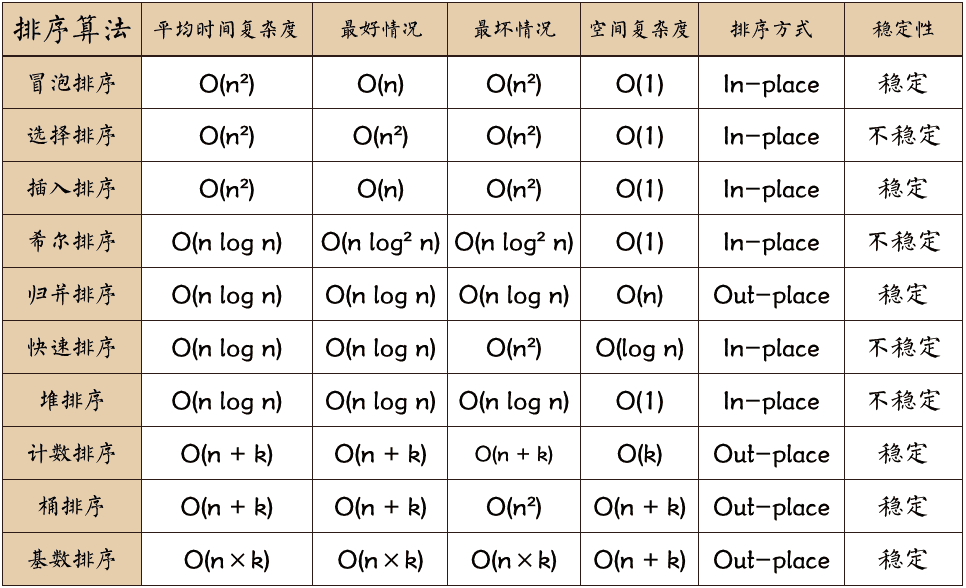
排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。用一张图概括：

sortSum

1. 冒泡排序

冒泡排序(Bubble Sort) 是一种简单直观的排序算法 . 他重复的走访需要排序的序列, 一次比较两个元素.如果顺序错误就将其对换. 循环往复直至没有数据可以对换位置.

1.1 算法步骤

比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

1.2 代码实现

const bubbleSort = (arr) =>{
  for(let i = 0;i< arr.length -1;i++){
    for(let j =0;j< arr.length -1;j++){
      if(arr[j] > arr[j+1]){
        [arr[j],arr[j+1]] = [arr[j+1],arr[j]];
      }
    }
  }
  return arr;
}

2. 选择排序

选择排序是一种直观简单的算法,无论什么数据其时间复杂度都是 O(n^2^)

2.1 算法步骤

首先在未排序的序列中找到最大(小) 的元素,将其放在排序序列的起始位置.
再从剩余的未排序数列中找到最大(小)的元素,将其放在已排序序列的末尾位置
重复第二部,直到所有元素均排序完成.

selectionSort

2.2 代码实现

export const selectionSort = (arr) => {
  for (let i = 0; i < arr.length; i++) {
    let minIndex = i;
    for (let j = i + 1; j < arr.length; j++) {
      minIndex = arr[minIndex] > arr[j] ? j : minIndex;
    }
    [arr[minIndex], arr[i]] = [arr[i], arr[minIndex]];
  }
  return arr;
};

3.插入排序

插入排序虽然没有冒泡排序和选择排序那么简单,但它的原理也是最容易理解的.插入排序是一种简单直观的排序方法,它的工作原理是通过构建有序序列,对未排序的序列数据,从后向前扫描,找到相应位置进行插入.

3.1 算法步骤

将第一个数据看做已排序序列,将第二个到最后一个数看做未排序序列.
从头到尾依次扫描未排序序列,将其插入到已扫描队列中.( 如果如某个元素相同,则放在这个元素后面)

insertionSort

3.2 代码实现

export const insertionSort = (arr) => {
  for (let i = 1; i < arr.length; i++) {
    let preIndex = i - 1;
    let cur = arr[i];
    while (preIndex >= 0 && arr[preIndex] > cur) {
      arr[preIndex + 1] = arr[preIndex];
      preIndex--;
    }
    arr[preIndex + 1] = cur;
  }
  return arr;
};

4.归并排序

归并排序(Merge Sort)是一种建立在归并操作上的有效的排序算法. 该算法是采用分治法( Divide and Conquer) 的一个非常典型的应用. 作为一种典型的分而治之思想的算法应用，归并排序的实现由两种方法：

自上而下递归（所有递归的方法都可以用迭代重写，所以就有了第 2 种方法）
自下而上迭代

和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是 O(nlogn) 的时间复杂度。代价是需要额外的内存空间。

4.1 算法步骤

申请空间,使其大小为两个已经排序序列之和, 该空间用来存放已经排序的序列
设定两个指针,最初位置分别为两个已排序序列的起始位置
比较元素,将较小的移入空间,并将指针向右移动
重复 3 直到某一排序指针到达末尾
将剩余部分填入末尾

4.2 代码实现

export const mergeSort = (arr) => {
  if (arr.length < 2) return arr;

  let middle = Math.floor(arr.length / 2);
  let left = arr.slice(0, middle);
  let right = arr.slice(middle);

  return merge(mergeSort(left), mergeSort(right));
};

const merge = (left, right) => {
  let res = [];

  while (left.length && right.length) {
    if (left[0] < right[0]) {
      res.push(left.shift());
    } else {
      res.push(right.shift());
    }
  }
  if (right.length) {
    res = res.concat(right);
  }
  if (left.length) {
    res = res.concat(left);
  }
  return res;
};

5 快速排序

快速排序是东尼·霍尔发明的算法. 在平均的状况下,排序 n 个项目需要 O(nlogn)次比较. 在最坏的情况下需要 O(n^2^)次比较,但这种情况很少出现.事实上，快速排序通常明显比其他 Ο(nlogn) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来。快速排序采用分治法(divide and conquer) 策略来把一个 List 分为两个子串. 快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看，快速排序应该算是在冒泡排序基础上的递归分治法。快速排序的名字起的是简单粗暴，因为一听到这个名字你就知道它存在的意义，就是快，而且效率高！它是处理大数据最快的排序算法之一了。为什么呢? 在《算法艺术与信息学竞赛》有这样一段话

快速排序的最坏运行情况是 O(n²)，比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn)，且 O(nlogn) 记号中隐含的常数因子很小，比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以，对绝大多数顺序性较弱的随机数列而言，快速排序总是优于归并排序。

5.1 算法步骤

从数列中挑选出一个元素,称为基准 “基准”（pivot)
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；

qucikSort

5.2 代码实现

export const quickSort = (arr) => {
  _quickSort(arr, 0, arr.length - 1);
  return arr;
};

const _quickSort = (arr, left, right) => {
  if (left < right) {
    let index = partition(arr, left, right);
    _quickSort(arr, left, index - 1);
    _quickSort(arr, index + 1, right);
  }
};

const partition = (arr, left, right) => {
  let pivot = arr[left];
  let i = left,
    j = right;

  while (i < j) {
    while (i < j && arr[j] >= pivot) {
      j--;
    }
    arr[i] = arr[j]; // 将小的数放到左边
    while (i < j && arr[i] <= pivot) {
      i++;
    }
    arr[j] = arr[i]; // 将大的数放到右边
  }
  //循环结束，i与j相等
  arr[i] = pivot;
  return i;
};